ACP Challenge 2016: Problem

The Torpedo Scheduling Problem: Description

Context

A schema of a steel production plant is given.

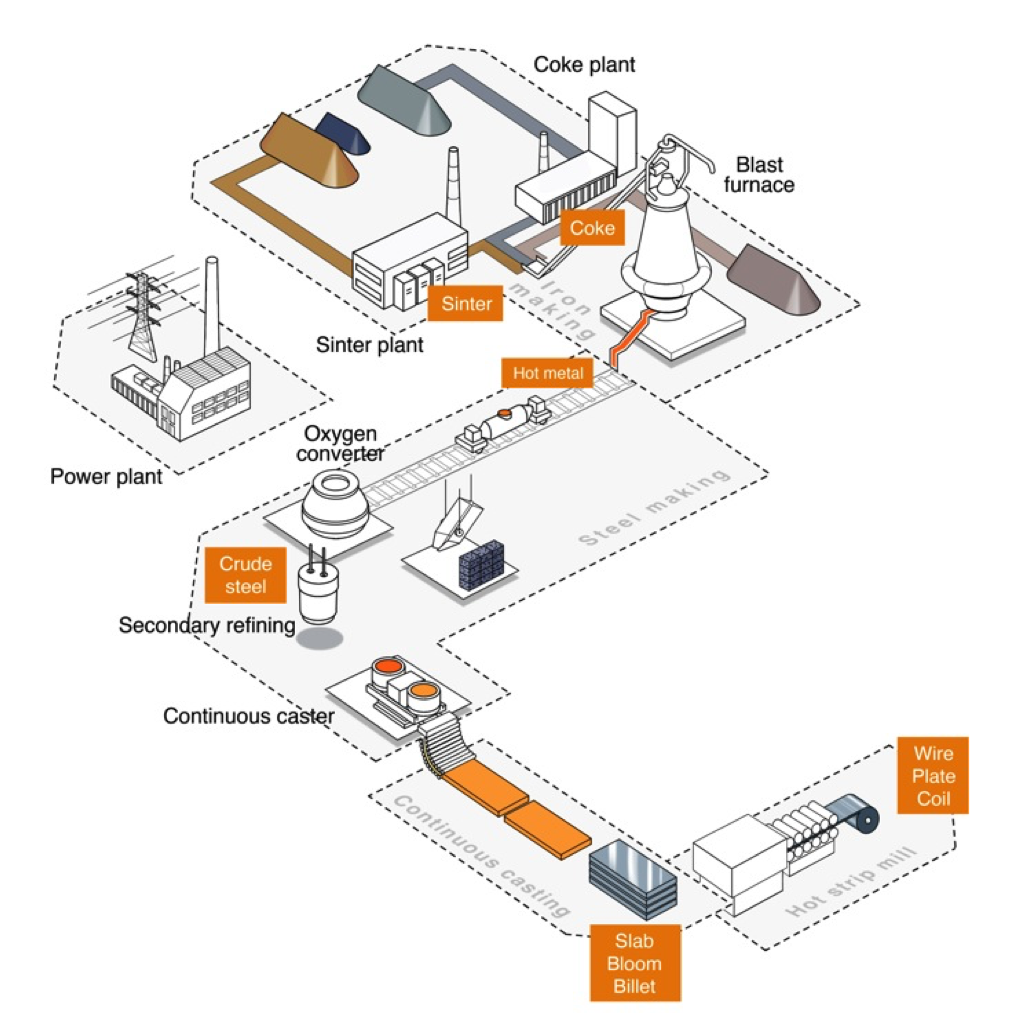
We are interested into the operations happening between the blast furnace (BF) and the oxygen converter (converter). The hot metal (HM) is transported into torpedo cars (torpedoes) between those two key components of the plant,

The goal of the problem is to schedule all the moves and operations of the torpedoes for the next hours.

Torpedo rotation

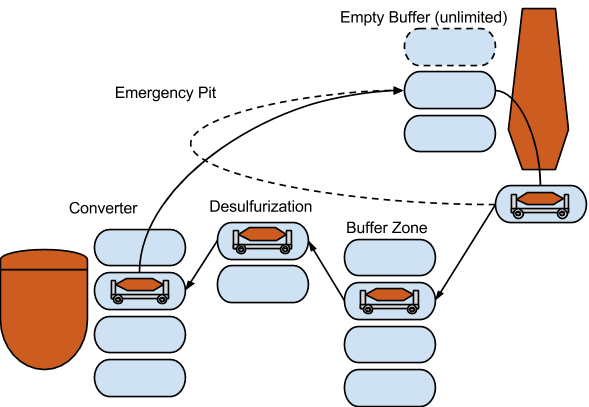
The rotation of a torpedo is depicted next.

The blast furnace (BF) continuously produces hot metal (HM) that is poured into torpedoes. Since the BF can never be stopped, there must always be a torpedo ready to accept HM metal under the BF. This is expressed as a set of due dates specified at the BF for the HM production. A due date means that an empty Torpedo must be ready at the BF to be filled in with a given level of sulfurization (integer number between 1 and 5). There is only one slot at the BF. It means that the next torpedo can arrive from the empty buffer at the BF only when the previous one has left. The empty torpedoes are waiting in the empty buffer zone that is uncapacitated. The empty buffer is also the place where all the torpedoes are located initially.

As soon as a torpedo becomes full, it is driven toward the converter. A set of due dates are specified at the converter. A due date at the converter means that a torpedo with a maximum specified level of sulfurization (number between 1 and 5) must be ready at the converter at that time. Its content will be poured into the converter at that date.

On its way to the converter, a first step is the capacitated full buffer, letting some flexibility to exchange orders. Then a desulfurization operation happens. This operation consists in adding calcium into the torpedo to cause a precipitation of the sulfur and decrease its sulfurization level.

Then the torpedo pours its content into the converter (What happens to the HM beyond this step is out of scope of the problem definition) and finally comes back to the empty buffer.

Desulfurization

In practice there are several BF’s, each is producing HM with a varying level of sulfurization. We assume they are 5 possibles levels from 1 (low) to 5 (high). A torpedo that receives a load with a (sulfurization) level i can decrease it to level i-1 by spending at least durDesulf unit of time at the desulfurization station. It can decrease it to level i-2 by spending at least 2*durDesulf unit of times, etc. The number of desulfurization stations is given in the input file as nbSlotsDesulf. This limits the number of simultaneous desulfurization. All the torpedoes must go through the desulfurization step after being loaded at the BF.

But the desulfurization duration can be as short as 0, in this case no utilization of the capacity is used. Assume for instance for instance a scenario with a desulfurization station with capacity 1 currently busy at processing a torpedo for a while. It is totally fine if another torpedo goes through the station without staying there (duration of 0) during the processing of the previous one.

Emergency pit

The BF continuously produces hot liquid metal. In case the demand throughput is not as high as the BF production rate or in case every torpedo is already full and there is urgency to consume the output of the BF, there is the possibility to get rid of hot liquid metal more rapidly using an emergency pit. It takes a fixed amount of time to use it and to get rid of the the content of the torpedo. In case a torpedo uses the emergency pit, it will bypass the converter step to pour its full content.

Transition times

Between any two locations, a minimum transition time is specified to move the torpedo from one place to the next. No two torpedoes can move at the same time between two locations except for the “emergency pit” transition which is uncapacitated.

Summary

A torpedo can follow two cycles:

BF -> Buffer Zone -> Desulfurization -> Converter -> Empty Buffer -> BF
BF -> Emergency Pit -> EmptyBuffer -> BF

The first cycle is the standard cycle. The second cycle is only useful in case the BF produces more than to fulfill the demands.

Objective function

The objective function is a lexicographic ordering of the following criteria:

1. Minimize the number of torpedoes
2. Minimize the total time spent at the desulfurization station

Input Data

Plant specific data

durBF=duration to fill in a torpedo with HM at the BF
durDesulf=duration to decrease by one level the desulfurization level of a torpedo
durConverter=duration to pour the content of the torpedo into the converter
nbSlotsFullBuffer=number of slots in the buffer zone
nbSlotsDesulf=number of desulfurization slots
nbSlotsConverter=number of converter  slots
ttBFToFullBuffer=min transition time from BF to full buffer
ttFullBufferToDesulf=min transition time from full buffer to desulf
ttDesulfToConverter=min transition time from desulf to converter
ttConverterToEmptyBuffer=min transition time from converter to empty buffer
ttEmptyBufferToBF=min transition time from empty buffer to bf
ttBFEmergencyPitEmptyBuffer=min transition time emergency pit, empty buffer

There are thus 5 different locations on a plant each with a different capacity (nbSlotsXXX):

• Empty Buffer (capacity = +infinity)
• BF (capacity = 1)
• Buffer Zone (capacity = nbSlotsFullBuffer)
• Desulfurization (capacity = nbSlotsDesulf)
• Converter (capacity = nbSlotsConverter)

The values (nbSlotsXXX) should really be seen this as a capacities (of discrete resources) since we do not distinguish the slots. Notice that the slots of the converter are at the converter location. A torpedo located at a converter slot is "at the converter". It’s next step is to come back at the empty buffer.

Instance Specific Data:

• a set of <’BF’, id, t, sulfurization level> at the BF. The BF starts to pour HM into a torpedo at time t during durBF units of time. Identifier id uniquely identifies this entry at the BF.
• a set of <’C’, id, t, maximum sulfurization level> at the converter. The torpedo starts to pour its content at time t at the converter during durConverter units of time. Identifier id uniquely identifies this entry at the Converter.

Example of input file 102.ins

durBF=5
durDesulf=5
durConverter=5
nbSlotsFullBuffer=4
nbSlotsDesulf=2
nbSlotsConverter=2
ttBFToFullBuffer=2
ttFullBufferToDesulf=1
ttDesulfToConverter=2
ttConverterToEmptyBuffer=4
ttEmptyBufferToBF=1
ttBFEmergencyPitEmptyBuffer=20
BF 0 5 3
BF 1 15 5
BF 2 25 3
BF 3 47 2
BF 4 70 3
C 0 30 2
C 1 57 1
C 2 62 1
C 3 80 3

Description of the solution

For each torpedo, one must describe all its moves chronologically.

The following example gives a solution with three torpedoes. The first one is doing two regular cycles, the second one two regular cycles, and the third one is doing a cycle using the emergency pit.

Notice that in case there are several possibilities because two torpedoes satisfies the sulfur level of a demand at the converter, the solution specifies without ambiguity which one will be chosen.

In the solution format, for each "regular" cycle, the assignment “BF production id (idBF) <-> Converter demand id (idConverter)” should be specified first.

Example of solution file 102.sol

102.ins
TeamsID=XMAMMA             # (cf. private keys provided by the registration form)
nbTorpedoes=3              # Total number of torpedoes

idTorpedo=0                # Torpedo id
idBF=0                     # BF production id
idConverter=0              # Converter demand id
startBF=5
endBF=10
startFullBuffer=12
endFullBuffer=22
startDesulf=23
endDesulf=28
startConverter=30
endConverter=35
startEmptyBuffer=39
endEmptyBuffer=42

idTorpedo=0
idBF=3
idConverter=2
startBF=47
endBF=52
startFullBuffer=54
endFullBuffer=54
startDesulf=55
endDesulf=60
startConverter=62
endConverter=67
startEmptyBuffer=71
endEmptyBuffer=89

idTorpedo=1
idBF=1
idConverter=1
startBF=15
endBF=20
startFullBuffer=22
endFullBuffer=30
startDesulf=31
endDesulf=51
startConverter=57
endConverter=62
startEmptyBuffer=66
endEmptyBuffer=69

idTorpedo=1
idBF=4
idConverter=3
startBF=70
endBF=75
startFullBuffer=77
endFullBuffer=77
startDesulf=78
endDesulf=78
startConverter=80
endConverter=85
startEmptyBuffer=89
endEmptyBuffer=89

idTorpedo=2
idBF=2
idConverter=-1
startBF=25
endBF=30
startEmptyBuffer=50
endEmptyBuffer=89

The objective function for this solution is:

#torpedoes=3
#timeDesulf=30

Since the objective function is lexicographic, the second objective (timeDesulf) will be normalized to have a value always between 0 and 1.

In the output of the checker you’ll see:

The ranking is based on this cost. More precisely it is on the gain wrt to a solution that would use one torpedo for every order at the BF: